統計にまつわる不思議な話-シンプソンのパラドックス-
准教授 青木優(物理学、情報学)
昔から不思議な話が大好きで、「どうしてだろう?」と、つい考え込んでしまいます。不思議な話にもいろいろあります。一般的には、超常現象、UFO・宇宙人、心霊現象、古代文明などの話が多いですが、私の場合、数学、物理学、化学、生物学などの自然科学に関する不思議な話に惹かれてしまいます。特に‘パラドックス(paradox)’という言葉には強く惹かれます。
今回は、みなさんにもその不思議さを味わってもらいたいと思い、統計学で有名な‘シンプソンのパラドックス’と呼ばれるパラドックスをご紹介します。
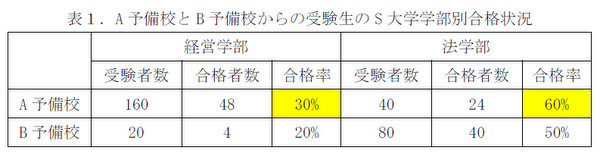
S大学は、経営学部と法学部の二学部で構成される大学です。そこにA予備校とB予備校から受験者が来ました。その合格状況を表1に示します。表1を見ると、A予備校は経営学部でも法学部でもB予備校よりも合格率が高く、S大学への合格率が高い予備校であると結論付けることができそうです。
昔から不思議な話が大好きで、「どうしてだろう?」と、つい考え込んでしまいます。不思議な話にもいろいろあります。一般的には、超常現象、UFO・宇宙人、心霊現象、古代文明などの話が多いですが、私の場合、数学、物理学、化学、生物学などの自然科学に関する不思議な話に惹かれてしまいます。特に‘パラドックス(paradox)’という言葉には強く惹かれます。
今回は、みなさんにもその不思議さを味わってもらいたいと思い、統計学で有名な‘シンプソンのパラドックス’と呼ばれるパラドックスをご紹介します。
S大学は、経営学部と法学部の二学部で構成される大学です。そこにA予備校とB予備校から受験者が来ました。その合格状況を表1に示します。表1を見ると、A予備校は経営学部でも法学部でもB予備校よりも合格率が高く、S大学への合格率が高い予備校であると結論付けることができそうです。
ところが、学部に分けて集計せずに、S大学全体で集計すると、表2のようにB予備校の方がS大学への合格率が高い予備校ということになります。このように、母集団全体から得られた結論と、母集団を分割して得られた結論が異なることを‘シンプソンのパラドックス’と言います。

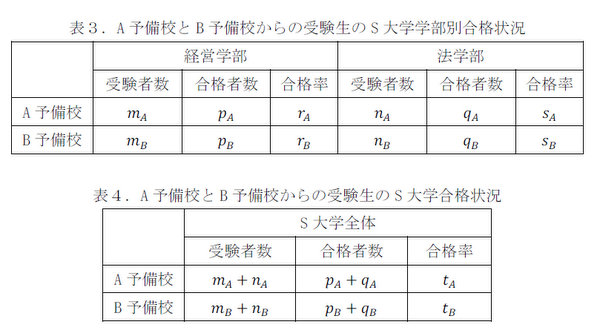
このような事がどうして起きるのか、以下に説明します。最初に、表1のデータを表3のように変数に置き換えます。すると表2のデータは、表4のようになります。
ここで、表4の合格率tA ,tB は、以下のように表すことができます。

この合格率tA ,tB の式を次のように変形してみます。
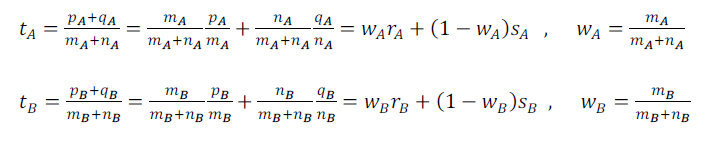
今、wA が1に近く、wB が0に近いとすると、次のようになります。

つまり、rA > rB かつ sA > sBであっても、sB > rAであれば、S大学への合格率はB予備校の方が大きくなることが分かります。
しかし、だからと言って、B予備校が受験生にとって良い予備校であるとは必ずしも言い切れません。これだけの情報では、どちらが良い予備校かは判断できません。
‘シンプソンのパラドックス’は如何でしたか。一言で’パラドックス’と言っても、いろいろな話があります。あなたの日常生活の中にも’パラドックス’は潜んでいるかも知れません。
しかし、だからと言って、B予備校が受験生にとって良い予備校であるとは必ずしも言い切れません。これだけの情報では、どちらが良い予備校かは判断できません。
‘シンプソンのパラドックス’は如何でしたか。一言で’パラドックス’と言っても、いろいろな話があります。あなたの日常生活の中にも’パラドックス’は潜んでいるかも知れません。
